基础知识：量子计算机如何运作及其技术发展方向

量子计算的理论基础贯穿整个二十世纪逐步形成，包括普朗克的量子假说（1900年）、不确定性原理（1927年）以及贝尔不等式（1964年）。其实际应用最早出现在1980年代，当时理查德·费曼提出利用量子系统模拟其他量子系统——这是经典计算机无法完成的任务。 这一构想催生了量子算法的研发，如肖尔算法（1994年）证明量子计算机能高效分解大数，以及格罗弗算法（1996年）——亦称量子搜索算法。与此同时，彼得·肖尔及其团队开发的量子纠错码，为实现量子计算的可行性奠定了重要基础。 自2000年以来，一场构建实用量子计算机的激烈竞赛持续展开，科技巨头与初创企业纷纷宣布在实现量子霸权方面取得进展。类似于集成电路容量的增长模式，量子计算能力可能呈现指数级增长（例如根据罗斯定律，芯片上的量子位数量约每18个月翻一番）。

量子计算机与经典计算机

量子计算机与经典计算机的运作原理存在根本差异。 经典计算机通过晶体管（或任何数字电路）处理信息，这些元件以二进制位存储数据。每个位仅能处于两种状态之一：0或1，分别对应晶体管栅极上电压的缺失或存在。这种二进制状态系统简单而可靠，确保测量晶体管状态时，其结果必然明确显示0或1。

相比之下，量子计算机利用量子比特（简称量子位）进行运算，这些量子位具有同时处于两种状态（分别标记为|0⟩和|1⟩）的概率。量子位可以像二进制那样工作，即被设定为0或1。然而，由于其量子力学特性，量子位能实现更强大的功能。 它们能处于叠加态，同时体现0和1的特性。布洛赫球体模型生动诠释了这一现象：与只能位于南北极（代表0或1）的经典比特不同，量子比特可存在于球体表面的任意位置，包括两极：

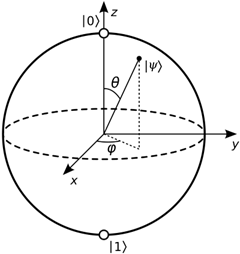
另一个类比是，经典比特可比作竖起大拇指或竖起小指的系统：拇指向上代表1，向下代表0。而量子比特则允许拇指在未完全竖起或放下的状态下仍能表示数值。 因此，当拇指处于特定角度|ψ>时（例如90度或任意方向的35度），该角度即代表量子比特的状态并能编码信息。而水平放置的拇指则同时表示|0⟩和|1⟩两种状态。

这种范式使量子比特能够同时呈现多种状态，从而导致概率性测量结果——根据量子比特的状态，测量出0或1的概率会发生变化。

有什么好处？

量子计算机能够同时处于多种状态，这使其能够以经典计算机无法企及的方式编码和处理信息。例如，当经典计算机的三个比特每次只能表示八种可能状态中的一种时，量子计算机却能在叠加态中同时表示全部八种可能状态。 这一概念（即量子并行性）结合量子干涉效应（即叠加态内各状态间的相互作用），使量子计算机能够以远低于经典计算机的硬件成本完成特定计算任务。这种数据处理方式的显著差异正是量子计算机的独特之处，它对量子计算机能够高效处理的任务类型和计算领域具有重大影响。

此外，量子计算机还受益于另一个重要概念——“量子纠缠”。量子计算中的纠缠使量子比特能够相互关联，从而以超越经典计算机能力的方式处理和存储信息。当一组量子比特（称为“纠缠量子比特”）共享量子态时，它们的属性便会产生关联，此时便形成了量子纠缠。 假设存在两个纠缠量子位。当量子计算机测量或改变其中一个量子位的属性（如自旋、位置或偏振）时，另一个量子位的属性会立即随之改变——因为它们的属性与状态处于关联或纠缠状态。 量子计算机可利用这种瞬时关联性提升处理能力。例如，这种相互关联性促进了并行计算，使量子计算机能够通过同时执行多项计算更高效地解决复杂问题。此外，纠缠效应还增强了量子算法的精度，在密码学、优化问题和材料科学等领域助力实现更快更精确的问题解决。

示例

为说明纠缠如何提升计算能力，请考虑以下示例：

在经典计算机中，位数的翻倍仅能使处理能力翻倍。也就是说，计算能力与位数呈线性增长。但在量子计算中，这种关系呈指数增长。因此，向一台60量子位的计算机添加一个额外的量子位，将使该量子计算机能够同时评估2⁶⁰个量子位状态。

正如经典门根据布尔逻辑以明确定义的方式操作比特，量子门通过量子门对量子比特进行操作，从而实现量子算法的执行。 因此，量子门堪称量子计算的基本构建模块，可视为经典计算中"逻辑门"的量子版本。与逻辑门不同，量子门能实现更复杂精妙的操作。例如，经典门对输入施加确定性变换，而量子门则引入纠缠与叠加等操作，通过非经典行为增强计算潜力。

量子门可用于量子算法中，通过操控量子比特来执行复杂计算。理解量子算法的运作机制，能令人惊叹地窥见量子计算的强大潜力。最初，量子计算机的输入通常由庞大的叠加态构成，这意味着系统同时呈现多种潜在结果。 基于量子并行性特性，各类量子门可同时作用于所有潜在状态。这种并行操作与量子干涉效应相辅相成——后者通过调整各状态的权重系数，进一步塑造计算过程。

下一步是什么？

量子计算技术正临近一个关键转折点，有望从实验室走向公众应用。迄今为止，该领域发展虽迅猛，但在公众应用层面仍显有限。 少数企业和研究机构已开发出增量式量子处理器，并将其集成到面向全球开发者的云平台中。这种可访问性使得量子算法实验成为可能，为未来应用奠定了基础。随着处理器量子位数量与稳定性的提升，以及纠错技术的改进，我们正接近一个临界点——量子计算将开始影响密码学、复杂分子建模和优化问题等领域。

尽管量子计算展现出巨大潜力，但预测其何时能实现大规模应用仍具挑战性。 该领域仍处于早期发展阶段，正面临量子比特相干性、错误率与纠错机制、可扩展系统设计等重大技术瓶颈。由于必须先攻克这些基础性难题，才能实现可靠且经济高效地将其融入日常技术，因此其广泛商业化的时间表尚不明朗。这种不确定性凸显了量子计算技术的实验性与渐进性特征——它正试图从实验装置向实用化的大众市场应用转型。

在后续文章中，我们将探讨量子计算技术如何通过迭代演进，逐步渗透到日常生活之中。

超越二元系列

点击此处查看福莱律师事务所的多篇系列文章《超越二进制》，该系列深入剖析量子计算技术的各个维度、其运作原理，以及围绕其发展与应用的法律环境。

要订阅本系列，请点击此处。