The Basics: How Quantum Computers Work and Where the Technology is Heading

The theoretical foundations of quantum computing emerged throughout the twentieth century, including Planck’s Quantum Hypothesis (1900), the Uncertainty Principle (1927), and Bell’s Inequality (1964). Practical applications initially emerged in the 1980s when Richard Feynman proposed using quantum systems to simulate other quantum systems, a task impractical for classical computers. This idea spurred the development of quantum algorithms, like Shor’s Algorithm (1994), which showed that quantum computers could efficiently factorize large numbers, and Grover’s Algorithm (1996), which is also known as the quantum search algorithm. Alongside this, the development of quantum error-correcting codes by Peter Shor and his colleagues marked significant progress in making quantum computing viable. Since 2000, an intense race to build practical quantum computers has ensued with technology behemoths and startups announcing advancements toward quantum supremacy. Similar to integrated circuit capacity, we may witness exponential growth in quantum computing capacity (e.g., the number of qubits on chips doubling about every 18 months per Rose’s Law).
Quantum Computers vs. Classical Computers
Quantum computers and classical computers operate on fundamentally different principles. Classical computers process information using transistors (or any digital circuitry) that store data in binary bits. These bits can only be in one of two states, either 0 or 1, which correspond to the absence or presence of voltage on the transistor gate. This binary state system is simple and robust, ensuring that when the state of a transistor is measured, it will distinctly show either a 0 or a 1.
In contrast, quantum computers utilize quantum bits – known as qubits – which have some probability of being in each of two states (designated |0⟩ and |1⟩) at the same time. Qubits can operate in binary in that they can be set to 0 or 1. However, due to their quantum mechanical nature, qubits can do much more. They can exist in a superposition state, where they embody aspects of both 0 and 1 simultaneously. This phenomenon is depicted in the Bloch Sphere, where unlike a classical bit that can only be at the North or South Pole (representing 0 or 1), a qubit can be anywhere on the sphere’s surface, including the poles:
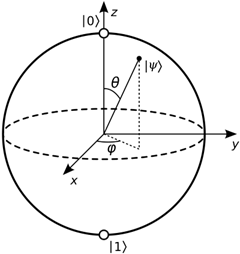
In another analogy, classical bits can be likened to a thumbs-up or thumbs-down system, where a thumb pointing up represents a 1 and a thumb pointing down represents a 0. On the other hand, a qubit allows for the thumb to represent a value even if it’s not completely up or down. Thus, a thumb positioned at an angle |ψ> which represents the qubit state, e.g., a 90-degree, or a 35-degree angle (in all directions), can also encode information. A thumb positioned horizontally represents a |0⟩ and |1⟩ at the same time.
This paradigm allows the qubit to represent multiple states at once, leading to probabilistic measurement outcomes where the likelihood of measuring a 0 or 1 can vary based on the qubit’s state.
What’s The Benefit?
The ability to exist in multiple states simultaneously enables quantum computers to encode and process information in ways that classical computers cannot. For instance, while a classical computer with three bits can represent one of eight possible states at a time, a quantum computer can represent all eight possible states simultaneously in a superposition state. This concept (i.e., quantum parallelism) along with quantum interference (i.e., the interaction between the states within a superposition), allows quantum computers to perform certain computations much faster and with less hardware than classical computers. This stark difference in data processing is what sets quantum computers apart, and it has significant implications for the kinds of tasks and calculations they can perform efficiently.
Additionally, quantum computers benefit from another important concept, “quantum entanglement.” Entanglement in quantum computing allows qubits to be interlinked, enabling them to process and store information in ways that surpass classical computers’ capabilities. Quantum entanglement occurs when a group of qubits (referred to as “entangled qubits”) share a quantum state so that their properties become correlated. Suppose there are two entangled qubits. When a quantum computer measures or changes a property of one qubit (e.g., spin, position, or polarization), it will then instantaneously change a property of the other qubit because their properties and states are correlated or entangled. Quantum computers can utilize this instantaneous correlation to improve their processing power. For instance, this interconnectedness facilitates parallelism, enabling quantum computers to solve complex problems more efficiently by performing multiple calculations simultaneously. Additionally, entanglement enhances the precision of quantum algorithms, contributing to faster and more accurate problem-solving in fields like cryptography, optimization, and material science.
Example
To illustrate how entanglement can improve the computing power, consider the following example:
In a classical computer, doubling the number of bits can merely double the processing power. That is, the computing power grows linearly in relation to the number of bits. In quantum computing, however, this relationship is exponential. Therefore, adding an additional qubit to a 60-qubit computer will result in the quantum computer to be able to evaluate 260 qubit states concurrently.
Just as classical gates manipulate bits in well-defined ways according to Boolean logic, quantum gates operate on qubits using quantum gates, enabling the performance of quantum algorithms. Therefore, quantum gates are analogous to fundamental building blocks of quantum computing and can be thought of as a quantum version of the “logic gates” of classical computing. In contrast to logical gates, quantum gates can allow for more complex and nuanced operations. For instance, while classical gates apply deterministic transformations to their inputs, quantum gates introduce operations like entanglement and superposition, enhancing computational potential through non-classical behaviors.
Quantum gates can be utilized in quantum algorithms to orchestrate and perform complex computations using qubits. Understanding how a quantum algorithm operates offers an intriguing glimpse into the power of quantum computing. Initially, the input to a quantum computer typically consists of a massive superposition state, which means the system simultaneously represents multiple potential outcomes. Various quantum gates can then interact with all these potential states at once due to the property of quantum parallelism. This simultaneous operation is complemented by quantum interference, which adjusts the coefficients of these states, further shaping the computational process.
What’s Next?
Quantum computing technology is nearing a pivotal moment where it could transition from research laboratories to public use. Progress so far has been rapid but relatively small with regard to public consumption. A few companies and research institutions have developed incremental quantum processors and integrated them into cloud-based platforms that are accessible to developers worldwide. This accessibility allows for experimentation with quantum algorithms, laying the groundwork for future applications. Moreover, as these processors grow in qubit count and stability, and as error correction improves, we are approaching a threshold where quantum computing could start impacting areas such as cryptography, complex molecular modeling, and optimization problems.
While quantum computing shows tremendous potential, predicting its availability for mass use remains challenging. The field is still in its early stages, grappling with significant technical hurdles such as qubit coherence, error rates and correction, and scalable system design. The timeline for widespread commercial availability is uncertain because these foundational challenges must be overcome before it can be reliably and cost-effectively integrated into everyday technology. This uncertainty underscores the experimental and evolutionary nature of quantum computing technology as it seeks to transition from experimental setups to practical, mass-market applications.
In upcoming articles we will explore how quantum computing technologies will iteratively evolve and gradually pervade everyday life.
Beyond The Binary Series
Click here to view Foley’s multi-part Beyond The Binary series of articles describing various aspects of quantum computing technology, its principles, and the legal landscape surrounding its development and implementations.
To subscribe to the series, click here.


